Voronoi算法、Delaunay三角剖分算法与网格细分算法研究

参考文档

[1]https://zhuanlan.zhihu.com/p/459884570
[2]https://www.zhihu.com/question/20317274
[3]https://www.cnblogs.com/shushen/p/5251070.html
[4]https://en.wikipedia.org/wiki/Voronoi_diagram
[5]https://en.wikipedia.org/wiki/Delaunay_triangulation
[6]https://blog.csdn.net/weixin_43693967/article/details/129468043

Beginning

Voronoi算法、Delaunay triangulation

根据[2]我们可知 德劳内三角剖分(Delaunay triangulation) 是 沃罗诺伊图(Voronoi diagram)的对偶图

因此 如果我们需要Voronoi图的话 就必定需要理解Delaunay算法

根据[2]可知 Voronoi算法的基本生成流程

01. 生成若干特定点集 (图1.1)
02. 基于特定点集 进行 德劳内三角剖分 (图1.2)
03. 每一个特定点 会与 其他若干特定点 组成 多个德劳内三角形, 生成这些三角形的外心 (图1.3)
04. 因是有限正方形 直接截取得到边界交点 同时 将边界交点和外心分别关联到对应的特定点 (图1.4)
05. 某一特定点的关联点 顺时针或逆时针相连就得到了Voronoi Cell 而将所有特定的关联点分别相连就得到了Voronoi图 (图1.5)

图1.1

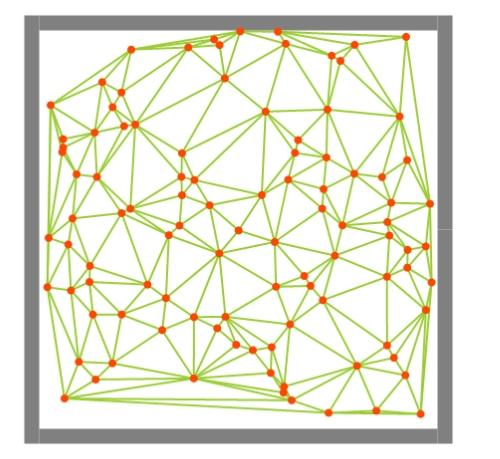
图1.2

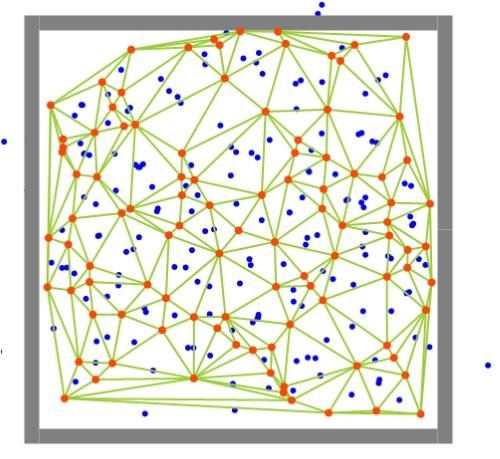
图1.3

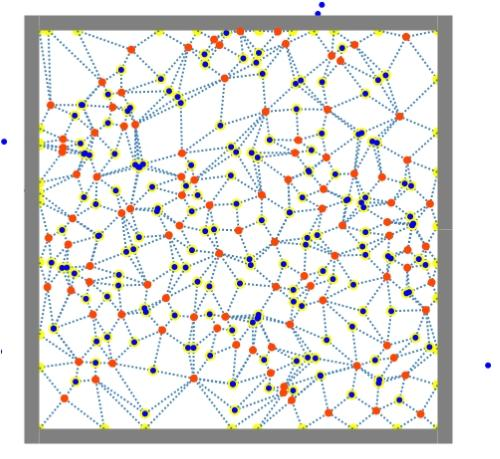
图1.4

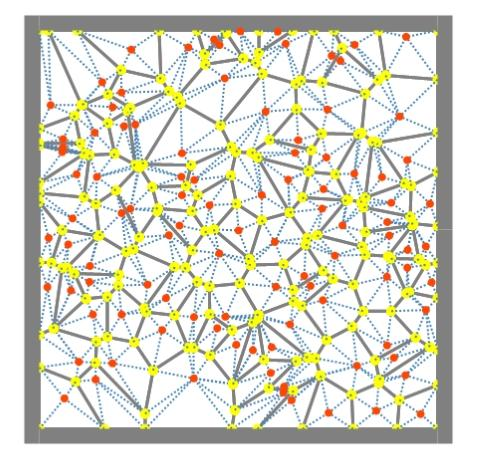
图1.5

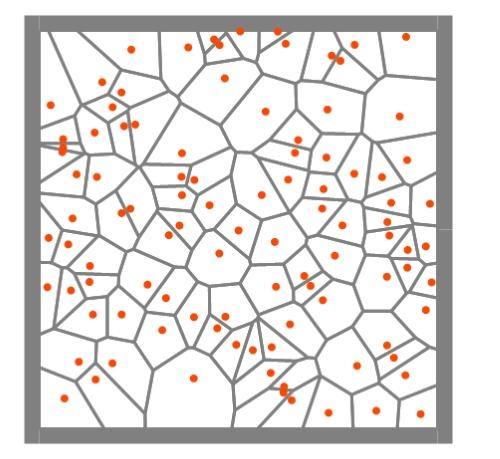
Voronoi 图

接下来 我们将使用一个开源库实现这部分

https://github.com/jbegaint/delaunay-cpp

这个库实现了Delaunay三角剖分 用Claude转换成UE的

// DelaunayTriangulation.h
// Bowyer-Watson algorithm implementation for Unreal Engine
// Based on http://paulbourke.net/papers/triangulate

#pragma once

#include "CoreMinimal.h"

namespace FDelaunayTriangulation
{
	constexpr float EPSILON = 1e-4f;

	// Edge structure
	struct FDelaunayEdge
	{
		FVector2D P0;
		FVector2D P1;

		FDelaunayEdge() : P0(FVector2D::ZeroVector), P1(FVector2D::ZeroVector)
		{
		}

		FDelaunayEdge(const FVector2D& InP0, const FVector2D& InP1)
			: P0(InP0), P1(InP1)
		{
		}

		bool operator==(const FDelaunayEdge& Other) const
		{
			return (P0.Equals(Other.P0) && P1.Equals(Other.P1)) ||
				(P0.Equals(Other.P1) && P1.Equals(Other.P0));
		}

		FString ToString() const
		{
			return FString::Printf(TEXT("Edge: P0(%s), P1(%s)"),
			                       *P0.ToString(), *P1.ToString());
		}
	};

	// Circle structure (circumcircle)
	struct FDelaunayCircle
	{
		FVector2D Center;
		float RadiusSquared;

		FDelaunayCircle() : Center(FVector2D::ZeroVector), RadiusSquared(0.0f)
		{
		}
	};

	// Triangle structure
	struct FDelaunayTriangle
	{
		FVector2D P0;
		FVector2D P1;
		FVector2D P2;
		FDelaunayEdge E0;
		FDelaunayEdge E1;
		FDelaunayEdge E2;
		FDelaunayCircle CircumCircle;

		FDelaunayTriangle(const FVector2D& InP0, const FVector2D& InP1, const FVector2D& InP2)
			: P0(InP0)
			  , P1(InP1)
			  , P2(InP2)
			  , E0(InP0, InP1)
			  , E1(InP1, InP2)
			  , E2(InP0, InP2)
		{
			CalculateCircumCircle();
		}

		void CalculateCircumCircle()
		{
			const float Ax = P1.X - P0.X;
			const float Ay = P1.Y - P0.Y;
			const float Bx = P2.X - P0.X;
			const float By = P2.Y - P0.Y;

			const float M = P1.X * P1.X - P0.X * P0.X + P1.Y * P1.Y - P0.Y * P0.Y;
			const float U = P2.X * P2.X - P0.X * P0.X + P2.Y * P2.Y - P0.Y * P0.Y;
			const float S = 1.0f / (2.0f * (Ax * By - Ay * Bx));

			CircumCircle.Center.X = ((P2.Y - P0.Y) * M + (P0.Y - P1.Y) * U) * S;
			CircumCircle.Center.Y = ((P0.X - P2.X) * M + (P1.X - P0.X) * U) * S;

			const float Dx = P0.X - CircumCircle.Center.X;
			const float Dy = P0.Y - CircumCircle.Center.Y;
			CircumCircle.RadiusSquared = Dx * Dx + Dy * Dy;
		}

		bool ContainsVertex(const FVector2D& Point) const
		{
			return P0.Equals(Point) || P1.Equals(Point) || P2.Equals(Point);
		}

		FString ToString() const
		{
			return FString::Printf(TEXT("Triangle: P0(%s), P1(%s), P2(%s)"),
			                       *P0.ToString(), *P1.ToString(), *P2.ToString());
		}
	};

	// Result structure
	struct FDelaunayResult
	{
		TArray<FDelaunayTriangle> Triangles;
		TArray<FDelaunayEdge> Edges;

		void Reset()
		{
			Triangles.Empty();
			Edges.Empty();
		}
	};

	// Main triangulation function
	inline FDelaunayResult Triangulate(const TArray<FVector2D>& Points)
	{
		FDelaunayResult Result;

		if (Points.Num() < 3)
		{
			return Result;
		}

		// Find bounding box
		float XMin = Points[0].X;
		float XMax = XMin;
		float YMin = Points[0].Y;
		float YMax = YMin;

		for (const FVector2D& Point : Points)
		{
			XMin = FMath::Min(XMin, Point.X);
			XMax = FMath::Max(XMax, Point.X);
			YMin = FMath::Min(YMin, Point.Y);
			YMax = FMath::Max(YMax, Point.Y);
		}

		const float Dx = XMax - XMin;
		const float Dy = YMax - YMin;
		const float DMax = FMath::Max(Dx, Dy);
		const float MidX = (XMin + XMax) * 0.5f;
		const float MidY = (YMin + YMax) * 0.5f;

		// Create super triangle that contains all points
		const FVector2D SuperP0(MidX - 20.0f * DMax, MidY - DMax);
		const FVector2D SuperP1(MidX, MidY + 20.0f * DMax);
		const FVector2D SuperP2(MidX + 20.0f * DMax, MidY - DMax);

		TArray<FDelaunayTriangle> Triangles;
		Triangles.Add(FDelaunayTriangle(SuperP0, SuperP1, SuperP2));

		// Add each point one at a time
		for (const FVector2D& Point : Points)
		{
			TArray<FDelaunayEdge> Edges;
			TArray<FDelaunayTriangle> TempTriangles;

			for (const FDelaunayTriangle& Triangle : Triangles)
			{
				// Check if point is inside the circumcircle
				const float DistSquared =
					FVector2D::DistSquared(Triangle.CircumCircle.Center, Point);

				if (DistSquared - Triangle.CircumCircle.RadiusSquared <= EPSILON)
				{
					// Point is inside circumcircle, add edges
					Edges.Add(Triangle.E0);
					Edges.Add(Triangle.E1);
					Edges.Add(Triangle.E2);
				}
				else
				{
					// Keep this triangle
					TempTriangles.Add(Triangle);
				}
			}

			// Remove duplicate edges
			TArray<bool> RemoveFlags;
			RemoveFlags.SetNumZeroed(Edges.Num());

			for (int32 i = 0; i < Edges.Num(); ++i)
			{
				for (int32 j = i + 1; j < Edges.Num(); ++j)
				{
					if (Edges[i] == Edges[j])
					{
						RemoveFlags[i] = true;
						RemoveFlags[j] = true;
					}
				}
			}

			TArray<FDelaunayEdge> UniqueEdges;
			for (int32 i = 0; i < Edges.Num(); ++i)
			{
				if (!RemoveFlags[i])
				{
					UniqueEdges.Add(Edges[i]);
				}
			}

			// Create new triangles from unique edges and the point
			for (const FDelaunayEdge& Edge : UniqueEdges)
			{
				TempTriangles.Add(FDelaunayTriangle(Edge.P0, Edge.P1, Point));
			}

			Triangles = MoveTemp(TempTriangles);
		}

		// Remove triangles that share vertices with super triangle
		Triangles.RemoveAll([&SuperP0, &SuperP1, &SuperP2](const FDelaunayTriangle& Triangle)
		{
			return Triangle.ContainsVertex(SuperP0) ||
				Triangle.ContainsVertex(SuperP1) ||
				Triangle.ContainsVertex(SuperP2);
		});

		// Build final result
		Result.Triangles = Triangles;

		// Extract all edges
		for (const FDelaunayTriangle& Triangle : Result.Triangles)
		{
			Result.Edges.Add(Triangle.E0);
			Result.Edges.Add(Triangle.E1);
			Result.Edges.Add(Triangle.E2);
		}

		return Result;
	}
} // namespace FDelaunayTriangulation

我们这回来写一个Voronoi diagram的实现

// VoronoiDiagram.h
// Voronoi diagram generation using Delaunay triangulation
// Requires DelaunayTriangulation.h

#pragma once

#include "CoreMinimal.h"
#include "DelaunayTriangulation.h"

namespace FVoronoiDiagram
{
	using namespace FDelaunayTriangulation;

	// Voronoi edge connecting two Voronoi vertices
	struct FVoronoiEdge
	{
		FVector2D P0;
		FVector2D P1;
		bool bIsInfinite; // For edges extending to infinity

		FVoronoiEdge() : P0(FVector2D::ZeroVector), P1(FVector2D::ZeroVector), bIsInfinite(false)
		{
		}

		FVoronoiEdge(const FVector2D& InP0, const FVector2D& InP1, bool bInfinite = false)
			: P0(InP0), P1(InP1), bIsInfinite(bInfinite)
		{
		}

		FString ToString() const
		{
			return FString::Printf(TEXT("VoronoiEdge: P0(%s), P1(%s)%s"),
			                       *P0.ToString(), *P1.ToString(), bIsInfinite ? TEXT(" [Infinite]") : TEXT(""));
		}
	};

	// Voronoi cell (region) for a single site point
	struct FVoronoiCell
	{
		FVector2D SitePoint; // Original point that this cell surrounds
		TArray<FVector2D> Vertices; // Voronoi vertices (circumcenters) in order
		TArray<FVoronoiEdge> Edges; // Edges of this cell

		FVoronoiCell() : SitePoint(FVector2D::ZeroVector)
		{
		}

		explicit FVoronoiCell(const FVector2D& InSitePoint) : SitePoint(InSitePoint)
		{
		}

		// Calculate area of the Voronoi cell (if closed)
		float CalculateArea() const
		{
			if (Vertices.Num() < 3)
			{
				return 0.0f;
			}

			float Area = 0.0f;
			for (int32 i = 0; i < Vertices.Num(); ++i)
			{
				int32 j = (i + 1) % Vertices.Num();
				Area += Vertices[i].X * Vertices[j].Y;
				Area -= Vertices[j].X * Vertices[i].Y;
			}
			return FMath::Abs(Area) * 0.5f;
		}

		// Get centroid of the cell
		FVector2D GetCentroid() const
		{
			if (Vertices.Num() == 0)
			{
				return SitePoint;
			}

			FVector2D Centroid = FVector2D::ZeroVector;
			for (const FVector2D& Vertex : Vertices)
			{
				Centroid += Vertex;
			}
			return Centroid / static_cast<float>(Vertices.Num());
		}

		FString ToString() const
		{
			return FString::Printf(TEXT("VoronoiCell: Site(%s), Vertices(%d)"),
			                       *SitePoint.ToString(), Vertices.Num());
		}
	};

	// Result structure
	struct FVoronoiResult
	{
		TArray<FVoronoiCell> Cells;
		TArray<FVoronoiEdge> AllEdges;
		FBox2D Bounds; // Bounding box used for clipping

		void Reset()
		{
			Cells.Empty();
			AllEdges.Empty();
			Bounds = FBox2D(ForceInit);
		}
	};

	// Sort vertices in counter-clockwise order around a center point
	inline void SortVerticesCounterClockwise(TArray<FVector2D>& Vertices, const FVector2D& Center)
	{
		Vertices.Sort([&Center](const FVector2D& A, const FVector2D& B)
		{
			const FVector2D VA = A - Center;
			const FVector2D VB = B - Center;
			const float AngleA = FMath::Atan2(VA.Y, VA.X);
			const float AngleB = FMath::Atan2(VB.Y, VB.X);
			return AngleA < AngleB;
		});
	}

	// Line segment intersection with bounding box
	inline bool ClipLineSegment(const FBox2D& Box, FVector2D& P0, FVector2D& P1)
	{
		// Cohen-Sutherland line clipping algorithm
		auto ComputeOutCode = [&Box](const FVector2D& P) -> uint8
		{
			uint8 Code = 0;
			if (P.X < Box.Min.X) Code |= 1; // Left
			if (P.X > Box.Max.X) Code |= 2; // Right
			if (P.Y < Box.Min.Y) Code |= 4; // Bottom
			if (P.Y > Box.Max.Y) Code |= 8; // Top
			return Code;
		};

		uint8 OutCode0 = ComputeOutCode(P0);
		uint8 OutCode1 = ComputeOutCode(P1);

		while (true)
		{
			if ((OutCode0 | OutCode1) == 0)
			{
				// Both points inside
				return true;
			}
			else if ((OutCode0 & OutCode1) != 0)
			{
				// Both points outside on same side
				return false;
			}
			else
			{
				// Line crosses boundary
				uint8 OutCodeOut = OutCode0 ? OutCode0 : OutCode1;
				FVector2D Intersection;

				if (OutCodeOut & 8) // Top
				{
					Intersection.X = P0.X + (P1.X - P0.X) * (Box.Max.Y - P0.Y) / (P1.Y - P0.Y);
					Intersection.Y = Box.Max.Y;
				}
				else if (OutCodeOut & 4) // Bottom
				{
					Intersection.X = P0.X + (P1.X - P0.X) * (Box.Min.Y - P0.Y) / (P1.Y - P0.Y);
					Intersection.Y = Box.Min.Y;
				}
				else if (OutCodeOut & 2) // Right
				{
					Intersection.Y = P0.Y + (P1.Y - P0.Y) * (Box.Max.X - P0.X) / (P1.X - P0.X);
					Intersection.X = Box.Max.X;
				}
				else if (OutCodeOut & 1) // Left
				{
					Intersection.Y = P0.Y + (P1.Y - P0.Y) * (Box.Min.X - P0.X) / (P1.X - P0.X);
					Intersection.X = Box.Min.X;
				}

				if (OutCodeOut == OutCode0)
				{
					P0 = Intersection;
					OutCode0 = ComputeOutCode(P0);
				}
				else
				{
					P1 = Intersection;
					OutCode1 = ComputeOutCode(P1);
				}
			}
		}
	}

	// Sutherland-Hodgman polygon clipping
	inline TArray<FVector2D> ClipPolygonToBox(const TArray<FVector2D>& Polygon, const FBox2D& Box)
	{
		if (Polygon.Num() < 3)
		{
			return TArray<FVector2D>();
		}

		TArray<FVector2D> Input = Polygon;
		TArray<FVector2D> Output;

		// Clip against each edge of the bounding box
		struct FClipEdge
		{
			FVector2D Normal;
			float Distance;
		};

		TArray<FClipEdge> ClipEdges;
		ClipEdges.Add({FVector2D(1, 0), Box.Min.X}); // Left
		ClipEdges.Add({FVector2D(-1, 0), -Box.Max.X}); // Right
		ClipEdges.Add({FVector2D(0, 1), Box.Min.Y}); // Bottom
		ClipEdges.Add({FVector2D(0, -1), -Box.Max.Y}); // Top

		for (const FClipEdge& Edge : ClipEdges)
		{
			Output.Empty();
			if (Input.Num() == 0)
			{
				break;
			}

			FVector2D PrevVertex = Input.Last();
			float PrevDot = FVector2D::DotProduct(PrevVertex, Edge.Normal) + Edge.Distance;

			for (const FVector2D& CurrentVertex : Input)
			{
				float CurrentDot = FVector2D::DotProduct(CurrentVertex, Edge.Normal) + Edge.Distance;

				if (CurrentDot >= 0)
				{
					if (PrevDot < 0)
					{
						// Entering - add intersection
						float T = PrevDot / (PrevDot - CurrentDot);
						FVector2D Intersection = PrevVertex + T * (CurrentVertex - PrevVertex);
						Output.Add(Intersection);
					}
					Output.Add(CurrentVertex);
				}
				else if (PrevDot >= 0)
				{
					// Leaving - add intersection
					float T = PrevDot / (PrevDot - CurrentDot);
					FVector2D Intersection = PrevVertex + T * (CurrentVertex - PrevVertex);
					Output.Add(Intersection);
				}

				PrevVertex = CurrentVertex;
				PrevDot = CurrentDot;
			}

			Input = Output;
		}

		return Output;
	}

	// Main Voronoi generation function
	inline FVoronoiResult GenerateVoronoi(const TArray<FVector2D>& Points,
	                                      const FBox2D& BoundingBox = FBox2D(FVector2D(-500, -500), FVector2D(500, 500)))
	{
		FVoronoiResult Result;
		Result.Bounds = BoundingBox;

		if (Points.Num() < 2)
		{
			return Result;
		}

		// Step 1: Generate Delaunay triangulation
		FDelaunayResult Delaunay = Triangulate(Points);
		if (Delaunay.Triangles.Num() == 0)
		{
			return Result;
		}

		UE_LOG(LogTemp, Log, TEXT("GenerateVoronoi: Processing %d points, %d triangles"),
		       Points.Num(), Delaunay.Triangles.Num());

		// Step 2: 为每条Delaunay边找相邻三角形（使用数组代替Map）
		struct FEdgeTrianglePair
		{
			FVector2D P0, P1;
			TArray<int32> TriangleIndices;
		};

		TArray<FEdgeTrianglePair> EdgeList;

		auto FindOrAddEdge = [&EdgeList](const FVector2D& A, const FVector2D& B) -> FEdgeTrianglePair*
		{
			FVector2D P0, P1;
			if (A.X < B.X || (FMath::IsNearlyEqual(A.X, B.X) && A.Y < B.Y))
			{
				P0 = A;
				P1 = B;
			}
			else
			{
				P0 = B;
				P1 = A;
			}

			for (FEdgeTrianglePair& Pair : EdgeList)
			{
				if (Pair.P0.Equals(P0, 0.1f) && Pair.P1.Equals(P1, 0.1f))
				{
					return &Pair;
				}
			}

			FEdgeTrianglePair NewPair;
			NewPair.P0 = P0;
			NewPair.P1 = P1;
			EdgeList.Add(NewPair);
			return &EdgeList.Last();
		};

		for (int32 i = 0; i < Delaunay.Triangles.Num(); ++i)
		{
			const FDelaunayTriangle& T = Delaunay.Triangles[i];
			FindOrAddEdge(T.P0, T.P1)->TriangleIndices.Add(i);
			FindOrAddEdge(T.P1, T.P2)->TriangleIndices.Add(i);
			FindOrAddEdge(T.P2, T.P0)->TriangleIndices.Add(i);
		}

		// Step 3: 为内部边生成Voronoi边
		for (const FEdgeTrianglePair& Edge : EdgeList)
		{
			if (Edge.TriangleIndices.Num() == 2)
			{
				FVector2D C0 = Delaunay.Triangles[Edge.TriangleIndices[0]].CircumCircle.Center;
				FVector2D C1 = Delaunay.Triangles[Edge.TriangleIndices[1]].CircumCircle.Center;

				if (ClipLineSegment(BoundingBox, C0, C1))
				{
					Result.AllEdges.Add(FVoronoiEdge(C0, C1));
				}
			}
		}

		UE_LOG(LogTemp, Log, TEXT("GenerateVoronoi: Generated %d edges"), Result.AllEdges.Num());

		// Step 4: 构建单元格
		Result.Cells.SetNum(Points.Num());
		for (int32 i = 0; i < Points.Num(); ++i)
		{
			Result.Cells[i] = FVoronoiCell(Points[i]);
		}

		return Result;
	}

	// Helper to create a square bounding box
	inline FBox2D MakeSquareBounds(float Size)
	{
		const float HalfSize = Size * 0.5f;
		return FBox2D(FVector2D(-HalfSize, -HalfSize), FVector2D(HalfSize, HalfSize));
	}

	// Helper to create a centered rectangular bounding box
	inline FBox2D MakeBounds(float Width, float Height)
	{
		const float HalfWidth = Width * 0.5f;
		const float HalfHeight = Height * 0.5f;
		return FBox2D(FVector2D(-HalfWidth, -HalfHeight), FVector2D(HalfWidth, HalfHeight));
	}

	// Helper to create a bounding box with custom origin
	inline FBox2D MakeBoundsWithOrigin(const FVector2D& Origin, float Width, float Height)
	{
		return FBox2D(Origin, Origin + FVector2D(Width, Height));
	}

	// Helper function to get neighboring cells
	inline TArray<int32> GetNeighboringCells(const FVoronoiResult& VoronoiResult, int32 CellIndex)
	{
		TArray<int32> Neighbors;
		if (!VoronoiResult.Cells.IsValidIndex(CellIndex))
		{
			return Neighbors;
		}

		const FVoronoiCell& Cell = VoronoiResult.Cells[CellIndex];

		// Find cells that share an edge with this cell
		for (int32 OtherIdx = 0; OtherIdx < VoronoiResult.Cells.Num(); ++OtherIdx)
		{
			if (OtherIdx == CellIndex)
			{
				continue;
			}

			const FVoronoiCell& OtherCell = VoronoiResult.Cells[OtherIdx];

			// Check if cells share at least 2 vertices (forming an edge)
			int32 SharedVertices = 0;
			for (const FVector2D& Vertex : Cell.Vertices)
			{
				for (const FVector2D& OtherVertex : OtherCell.Vertices)
				{
					if (Vertex.Equals(OtherVertex, 0.1f))
					{
						SharedVertices++;
						if (SharedVertices >= 2)
						{
							Neighbors.AddUnique(OtherIdx);
							break;
						}
					}
				}
				if (SharedVertices >= 2)
				{
					break;
				}
			}
		}

		return Neighbors;
	}
} // namespace FVoronoiDiagram

细分算法

细分算法我们着重研究Loop subdivision